Quiero investigar

Empezando a investigar

Índice del Curso

Tema 5 - Metodología

Tipos de estudios

Podemos distinguir varios criterios de clasificación (figura 6):

• Tipo de investigación:
  
• Cuantitativa.
• Cualitativa.
• Finalidad:
  
• Descriptivo.
• Analítico.
• Secuencia temporal o seguimiento:
  
• Transversal.
• Longitudinal.
• Control o manipulación:
  
• Experimental (intervención).
• Observacional.
• Inicio de estudio-cronología de los hechos:
  
• Prospectivo.
• Retrospectivo
  
  

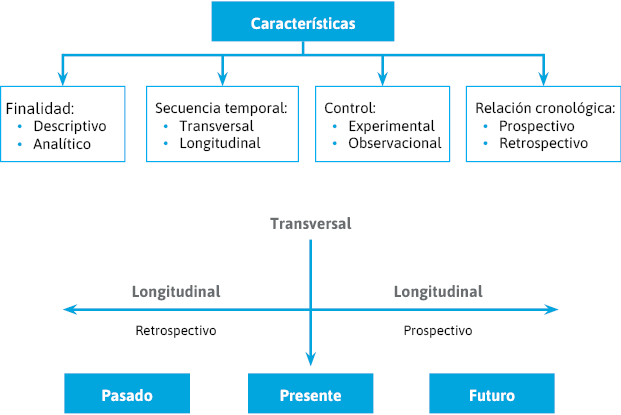
Figura 6. Tipos de estudio

Asimismo, es importante conocer las siguientes definiciones:

• Ensayo clínico: evaluación experimental de un producto, sustancia, medicamento, técnica diagnóstica o terapéutica que, en su aplicación a seres humanos, pretende valorar su eficacia y seguridad.
  
• Unidad de intervención/análisis:
  
• Individuo.
• Agregación de sujetos/poblaciones: centros de salud, provincias, etc.

En resumen, podemos hacer dos grandes grupos de estudios (figura 7):

• Observacionales:
  
• Descriptivos:
  
• Transversales: prevalencia, evaluación pruebas diagnósticas, concordancia, asociación cruzada, etc.
• Longitudinales: incidencia, descripción de la historia natural, etc.
• Analíticos:
  
• Casos y controles.
• Cohortes.
• Experimentales:
  
• Ensayo controlado aleatorio (ECA).
• Cuasi-experimental: ausencia de control (ENC) o de asignación aleatoria (ENA).

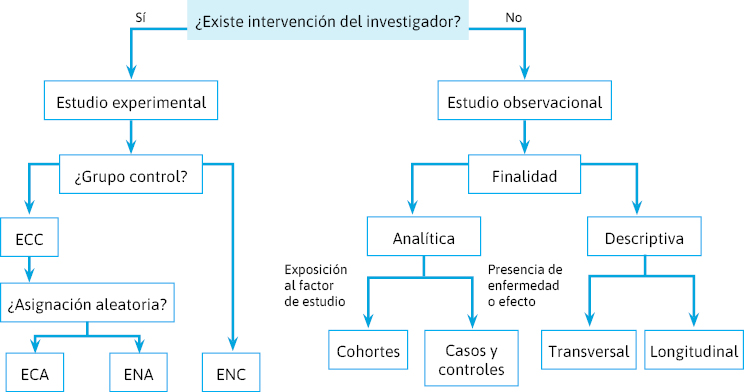
Figura 7. Grupos de estudios.

Estudios observacionales

Estudios observacionales no analíticos

Las principales características de los estudios descriptivos son (figura 8):

• Objetivo general:
  
• Describir la frecuencia y características de un problema de salud (enfermedad, factor de riesgo, prueba diagnóstica).
• Generar hipótesis.
• Prevalencia/incidencia: describen una serie de variables presentes/de nueva aparición. Por ejemplo: estimar los casos de portadores del virus de la hepatitis C en un momento dado.
  
• Series de casos: describen pacientes con características comunes poco conocidas. Por ejemplo: descripción de un conjunto de casos clínicos de portadores del virus de la hepatitis C que presenten un signo o síntoma poco frecuente o una exposición común.
  
• Estudios ecológicos (morbilidad/mortalidad): los sujetos de estudio son la agregación de personas (provincias, colegios, etc.) y no los individuos. Por ejemplo: descripción de la mortalidad por hepatopatía crónica en diferentes provincias, tomando como unidad de análisis las provincias y como datos el porcentaje de muertes por esta causa en cada provincia.
  

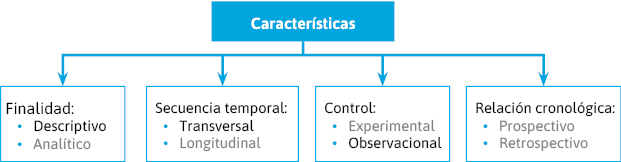
Figura 8. Estudios descriptivos

Los estudios transversales se caracterizan por (figura 9):

• Relación entre un problema y determinadas variables en un momento dado.
  
• El estatus de enfermedad y la exposición se observan simultáneamente.
  

Figura 9. Estudios transversales

Por ejemplo: estudiar la asociación entre obesidad y artrosis de rodilla. En el caso de que ambas variables estén asociadas, no podremos saber si las personas con artrosis son más obesas (porque hacen menos ejercicio) o si las personas obesas padecen más artrosis (por sobrecarga de la rodilla), ya que desconocemos la secuencia temporal. Tendríamos dos hipótesis de trabajo para confirmar en estudios longitudinales.

• Ventajas:
  
• Estimar la magnitud del problema (prevalencia) ⇒ planificación sanitaria.
• Analizar varios problemas o aspectos en un estudio.
• Corta duración ⇒ menos costosos.
• Primer paso ⇒ generación de hipótesis.
• Inconvenientes:
  
• No son útiles para enfermedades poco frecuentes.
• No hay causalidad: falta de secuencia temporal.
• Sesgos: selección («no respuestas»), supervivencia.

Estudios observacionales analíticos

El objetivo general de los estudios observacionales analíticos es evaluar una posible relación causa-efecto:

• Proporción de exposición al factor de riesgo (FR) entre enfermos y no enfermos (odds ratio: OR): relación entre la probabilidad de enfermar frente a la de no enfermar en expuestos y la probabilidad de enfermar frente a la de no enfermar en no expuestos ⇒ casos y controles.
  
• Incidencia de enfermedad en expuestos frente a no expuestos (riesgo relativo [RR] y riesgo absoluto [RA]) ⇒ cohortes.
  

En los estudios de casos y controles, la selección de los grupos se realiza en función del estatus de enfermedad (figura 10 y 11).


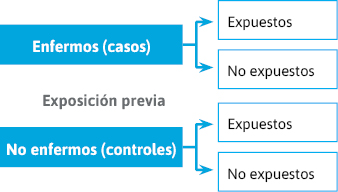
Figura 10. Estudios observacionales analíticos

Por ejemplo: estudiar si la vacunación antigripal previene la aparición de neumonías.
Se definiría como caso toda persona > 65 años no institucionalizada, residente durante más de 6 meses en el área de influencia del Hospital Universitario Reina Sofía (HURS), ingresada en el período de estudio por neumonía.
Se definiría como control a personas > 65 años no institucionalizadas, residentes durante más de 6 meses en el área de influencia del HURS, ingresadas en un período de tiempo de 7 días del ingreso del caso, por un proceso no neumónico (por ejemplo: proceso agudo quirúrgico o traumatismo).
Cada caso se aparearía con cada control en sexo, edad y semana de ingreso.
Se revisará cuántos casos y cuántos controles recibieron la vacunación antigripal (y, si se quiere, se pueden estudiar también otros factores que potencialmente puedan influir en la aparición de neumonía).


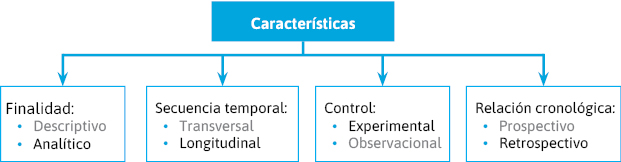
Figura 11. Casos y controles

En los estudios de casos y controles hay que analizar:

• ¿Asociación? Significación estadística:
  
• Proporción de expuestos en casos frente a proporción de expuestos en controles: ji-cuadrado.
• ¿Fuerza?: 
  
• Magnitud: odds ratio (OR=(a x d) / (b x c)).
• ¿Precisión?: 
  
• Intervalo de confianza al 95% (IC 95%) de la OR.
• ¿Confusión?:
  
• Análisis estratificado y/o multivariante.

OR: probabilidad de que los casos estén expuestos al factor de riesgo (FR) comparada con la probabilidad de que lo estén los controles.
El predominio es una relación entre dos probabilidades: hay un predominio en presencia del factor (PRF) y otro en ausencia del mismo (PRN).
El PRF es la razón entre la probabilidad de padecer la enfermedad (o presentar la característica de estudio) en presencia del factor y la probabilidad de no padecerla en presencia del mismo; conceptualmente, el PRF indica cuántas veces es más probable padecer la enfermedad que no padecerla cuando se está expuesto al factor.
El PRN es la razón entre la probabilidad de padecer la enfermedad (o presentar la característica de estudio) en ausencia del factor y la probabilidad de no padecerla en ausencia del mismo; conceptualmente, el PRN indica cuántas veces es más probable padecer la enfermedad que no padecerla cuando no se está expuesto al factor.
La razón entre los dos predominios (PRF/PRN) es la razón de predominio u OR: si no existe relación entre el factor y la enfermedad, el valor de la OR es estadísticamente igual a 1; si el factor es de riesgo, la OR es significativamente mayor de 1, y si el factor es de protección, la OR es significativamente menor de 1.

A continuación se resumen las ventajas e inconvenientes de los estudios de casos y controles:

• Ventajas:
  
• Útiles para enfermedades poco frecuentes y/o con largo período de latencia.
• Permite examinar varios factores de riesgo en un estudio.
• Corta duración ⇒ menos costosos.
• Inconvenientes:
  
• Solo se puede estudiar una enfermedad.
• Facilidad de incurrir en sesgos de selección e información: extremo cuidado en el diseño (los controles se escogerán de aquellos que, de haber desarrollado la enfermedad, hubiesen podido ser seleccionados como casos).

En los estudios de cohortes la selección se realiza en función del estatus de exposición (figuras 12 y 13):


Figura 12. Selección de estudios de cohortes

Por ejemplo: estudiar la relación entre exposición al asbesto y la aparición de cáncer de pulmón.
Se realiza un seguimiento durante 15 años de dos grupos de trabajadores de una empresa para ver cuántos desarrollan cáncer de pulmón: un grupo de los que trabajan en un departamento con exposición al asbesto y otro grupo de los que trabajan en un departamento sin exposición al asbesto.
La selección de registros de trabajadores expuestos y no expuestos en el pasado (1950), así como el registro en historias clínicas del padecimiento de cáncer de pulmón algún tiempo después (1965), constituye un abordaje del mismo problema desde un diseño de cohortes retrospectivo.


Figura 13 Estudios de cohortes

Se pueden encontrar dos subtipos de estudios de cohortes:

• Prospectivos:
  
• Se sigue a los sujetos (expuestos y no expuestos) para ver si presentan o no la enfermedad.
• Retrospectivos (cohortes históricas):
  
• Se selecciona a los sujetos y se reconstruye su historia a partir de registros existentes (el problema es que los registros no suelen estar diseñados para ese fin).

A continuación, se resumen las ventajas e inconvenientes de los estudios de cohortes:

• Ventajas:
  
• Secuencia temporal correcta: exposición ⇒ efecto.
• Calculamos directamente la incidencia ⇒ RR y RA.
• Examinar varios efectos de la misma exposición.
• Errores minimizados (prospectivos).
• Inconvenientes:
  
• No son útiles para enfermedades/exposiciones poco frecuentes.
• Sesgos por pérdidas de seguimiento (prospectivos).
• Eficiencia baja: larga duración, gran número de participantes Þ coste elevado.

Estudios experimentales

El objetivo general de los estudios experimentales es analizar una intervención específica aplicada de forma deliberada sobre un grupo de sujetos (figura 14).

Se puede evaluar la eficacia de intervenciones preventivas, curativas o rehabilitadoras.

Se suelen distinguir los siguientes subtipos de estudios experimentales:

• Cuasi-experimentales (de intervención):
  
• Ausencia de grupo control: estudios antes-después (cada sujeto es su propio control). No se puede asegurar que los cambios sean debidos exclusivamente a la intervención.
• Ausencia de asignación aleatoria: se asume que ambos grupos son similares, pero pueden diferir en variables no conocidas.
• Ensayos clínicos controlados (ECC) o aleatorizados (ECA):
  
• Grupo control diferente al de la intervención.
• Asignación aleatoria (randomización): cada individuo tiene la misma probabilidad de ser asignado a uno de los grupos.

Figura 14 Estudios experimentales

Existen varios condicionantes en los estudios experimentales:

• Garantizar la comparabilidad: los miembros de ambos grupos deben ser similares en todo, excepto en el tipo de intervención a evaluar.
  
• Idealmente, la evaluación debe realizarse sin conocer si el sujeto pertenece o no al grupo de intervención.
  
• Requerimientos éticos/legales:
  
• Consentimiento informado previo a la entrada.
• Aplicación de normas de buena práctica clínica (BPC) y principios éticos internacionales.
• Aplicación de la normativa vigente.

A continuación se resumen las ventajas e inconvenientes de los estudios de cohortes:

• Ventajas:
  
• Mayor control: 
• Factor de estudio y pronóstico.
• Aislamiento del efecto (mayor evidencia).
• Validez interna.
• Inconvenientes:
  
• Restricciones éticas.
• Validez externa.
• Coste elevado.

¿Qué diseño elijo?

• Cada uno tiene su papel:
  
• Series de casos ⇒ llamar la atención.
• Transversales ⇒ extensión del problema.
• Casos-controles ⇒ identificar los actores.
• Cohortes/experimentales ⇒ testar.
• Todos presentan ventajas y limitaciones.
  
• Decidir según el objetivo y la factibilidad.
  

Niveles de evidencia

1a: Metanálisis o revisión sistemática (RS) de ECA homogéneos.
1b: ECA con intervalos de confianza estrechos.
2a: RS de estudios de cohortes homogéneos.
2b: Estudio de cohortes o ECA de baja calidad.
2c: Estudios ecológicos.
3a: RS de estudios de caso-control (CC) homogéneos.
3b: Estudio de CC.
4: Serie de casos o cohortes, o CC de baja calidad.
5: Opinión de expertos sin valoración crítica explícita

Grados de recomendación

A. Extremadamente recomendable: basada en estudios de nivel de evidencia 1.
B. Recomendación favorable: basada en estudios de nivel 2 o 3 o en extrapolaciones de estudios de nivel 1.
C. Recomendación favorable, pero no de forma conclusiva: basada en estudios de nivel 4 o en extrapolaciones de estudios de nivel 2 o 3.
D. Ni recomienda ni desaprueba: basada en estudios de nivel 5 o no concluyentes o inconsistentes de cualquier nivel.

Si a la hora de evaluar las evidencias existe la dificultad de aplicar los resultados a nuestro medio, se pueden utilizar las «extrapolaciones». Esta técnica supone siempre un descenso de nivel de evidencia, y se puede llevar a cabo cuando el estudio del cual surge la evidencia presenta diferencias clínicamente importantes, pero existe cierta plausibilidad biológica con respecto a nuestro escenario clínico.
Cuando no se encuentra información que permita constatar un nivel de evidencia sobre un aspecto determinado o se trata de aspectos organizativos o logísticos, la recomendación se establece por consenso del grupo de trabajo.

Estudios cualitativos

Se suelen distinguir los siguientes tipos de estudios cualitativos:

• Observación.
  
• Entrevistas en profundidad.
  
• Grupos focales o de discusión.
  
• Métodos de consenso:
  
• Técnica de grupo nominal.
• Técnica Delphi.
• Tormenta de ideas (brainstorming).

Grupos focales

«Una reunión de un grupo de individuos seleccionados por los investigadores para discutir y elaborar, desde la experiencia personal, una temática o hecho social que es objeto de investigación» (Kerman).

Se pueden distinguir las siguientes etapas en el proceso del grupo focal:

1. Seleccionar moderador/es.
   
2. Definición de los objetivos:
   
• Guion de desarrollo:
  
• Identificar, analizar, formular y evaluar el problema de investigación.
• Definir un marco de referencia teórico-metodológico.
• Guía de temáticas-preguntas a desarrollar.
  
3. Desarrollo del taller: inducción, conducción y discusión grupal.
   
4. Clausura del taller: presentación de las conclusiones y acuerdos.
   
5. Proceso de validación de los acuerdos y resultados por parte del equipo investigador.
   
6. Informe final. 
   

Podemos ver un ejemplo de estudio híbrido en la figura 15.


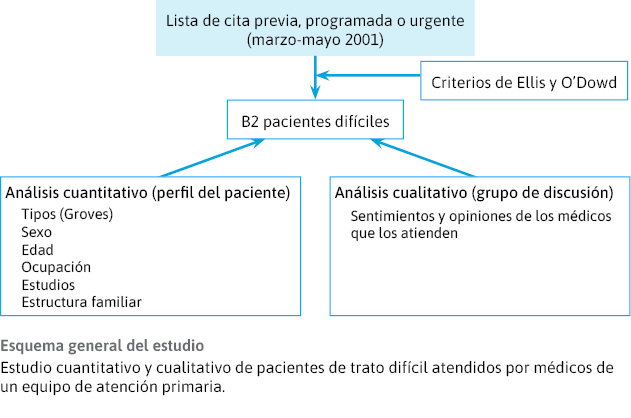
Figura 15. Ejemplo de estudio «híbrido», con una fase cualitativa y otra cuantitativa

Selección de la población de estudio

Se distinguen los siguientes niveles de población (figura 16):

• Pregunta de investigación ⇒ población diana.
  
• Accesibilidad/viabilidad ⇒ población accesible.
  
• Criterios de selección ⇒ población elegible.
  
• Tipo y tamaño muestral ⇒ muestra.
  
• No colaboración/pérdidas ⇒ participantes.
  

Población diana

Viene determinada por la pregunta de investigación, delimitada por las siguientes características:

• Demográficas (por ejemplo: mujeres en edad fértil [problemas de fertilidad]).
  
• Sociales (por ejemplo: desempleados [relación entre problemas de salud mental y desempleo])
  
• Referidas a hábitos (por ejemplo: consumidores de drogas por vía parenteral y virus de inmunodeficiencia humana [VIH]).
  
• Clínicas (por ejemplo: evaluación del programa de deshabituación tabáquica en sujetos con infarto agudo de miocardio [IAM]).
  
• Fisiológicas: tabaquismo pasivo en embarazadas.
  

Población accesible

Viene determinado por consideraciones prácticas en función de accesibilidad a los sujetos, existencia de registros, circunstancias que faciliten la colaboración, calidad de los datos, seguimiento, etc. Puede constar de:

• Pacientes que acuden al hospital.
  
• Embarazadas que asisten a las clínicas prenatales.
  
• Usuarios de drogas tratados en centros de deshabituación.
  
• Adolescentes en centros de enseñanza media.
  
• Residentes empadronados en un municipio.
  

Población elegible

Viene definida por los criterios de selección (criterios de inclusión y de exclusión). Estos criterios son decididos por el equipo investigador.

Muestra/participantes

• Muestra: subgrupo de la población elegible en el que vamos a realizar nuestro estudio.
  
• Participantes: subgrupo de la muestra determinado por:
  
• Rechazo a colaborar.
• Pérdidas en el reclutamiento.
• Pérdidas en el seguimiento 

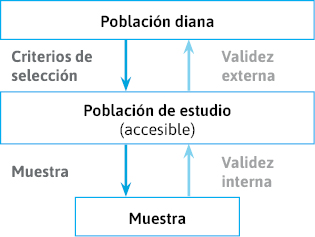
Figura 16. Distintos niveles de población

Los criterios de selección definen la población de estudio, de la que extraeremos nuestra muestra. Se distinguen:

• Criterios de inclusión:
  
• Características de la población elegible.
• Determinados por la pregunta de investigación.
• Criterios de exclusión:
  
• Subconjuntos de individuos que cumplen los criterios de inclusión, pero que es probable que interfieran en la calidad de los datos o en la interpretación de los hallazgos,
• No deben ser el «espejo» de los criterios de inclusión. Por ejemplo: no sería adecuado definir como criterio de inclusión «mujeres» y como criterio de exclusión «hombres», ya que lo segundo es evidente (criterios mutuamente excluyentes).

Consideraciones para elegir los criterios de selección

• Optimizar las posibilidades de detectar el efecto.
  
• Muestra homogénea respecto a las características más relevantes del fenómeno de estudio.
  
• No diferir mucho de la población diana a la que se van a generalizar los resultados.
  
• Realistas: deben permitir la inclusión del número de sujetos necesarios en el tiempo previsto.
  
• No olvidar los aspectos éticos.
  

Actitudes para elegir los criterios de selección

• Explicativa (eficacia): criterios muy estrictos ⇒ población homogénea, buena cumplidora:
  
• Ventaja: fácil encontrar un efecto/asociación, si existe.
• Problema: resultado poco generalizable.
• Pragmática (efectividad): criterios de selección amplios ⇒ población heterogénea:
  
• Ventaja: resultados generalizables.
• Problema: se pierde control sobre el estudio Þ mayor dificultad para hallar un efecto/asociación, si existe.

Por ejemplo: comparar un nuevo antihipertensivo (A) con uno conocido (B):

• Explicativa: efecto del fármaco en condiciones ideales (eficacia). Solo analizaremos aquellos pacientes que hayan tomado el fármaco tal como se indica en el protocolo y de los que tengamos al menos una evaluación postratamiento (análisis por protocolo).
  
• Pragmática: efecto del fármaco en condiciones reales (práctica clínica habitual). Se analizarán todos los pacientes que cumplen los criterios de inclusión, incluyendo los incumplidores, los que deben abandonar por efectos secundarios, etc., como fracasos del tratamiento (análisis por intención de tratar).
  

Categorías de criterios de selección

• Características sociodemográficas: edad, sexo, nivel socioeconómico, nivel cultural, etc.
  
• Características de la enfermedad o exposición (definición, forma, tipo, etc.).
  
• Ámbito geográfico y temporal.
  
• Otras: 
  
• Embarazo-lactancia.
• Hábitos tóxicos.

Tamaño de la muestra

Indica el número mínimo de sujetos que han de incluirse en el estudio para responder a las siguientes cuestiones (figura 17):

• ¿Cuántos son necesarios para poder estimar el parámetro de estudio con el grado de confianza deseado?
  
• ¿Cuántos son necesarios para poder detectar una determinada diferencia entre los grupos de estudio, en el supuesto de que esta diferencia exista realmente?
  

Hay que tener en cuenta las siguientes consideraciones:

• Criterio de eficiencia:
  
• Número excesivo: gasto de recursos innecesario, problemas éticos.
• Número escaso: estimaciones poco precisas, incapacidad para detectar diferencias.
• El cálculo es orientativo: se basa en asunciones que pueden ser incorrectas.
  
• Ha de fijarse previamente al desarrollo del estudio.
  

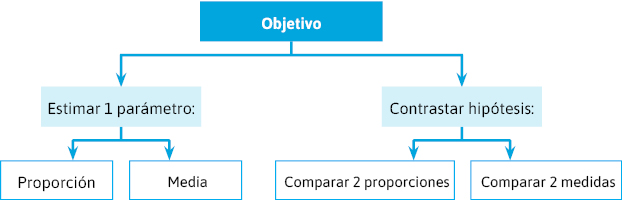
Figura 17. Consideraciones previas

• Estudios descriptivos: estimación de parámetros. ¿Cuántos sujetos son necesarios para poder estimar un parámetro (proporción o media) con un nivel de confianza deseado?
  
• Estudios analíticos: contraste de hipótesis. ¿Cuántos sujetos son necesarios para tener las mínimas garantías de poder detectar una determinada diferencia entre los grupos de estudio en el supuesto de que ésta exista realmente?
  

Estimación de 1 parámetro

• Intervalos de confianza (IC):
  
• Aquel intervalo que tiene una elevada probabilidad de contener el verdadero valor poblacional.
• Amplitud del IC ⇒ precisión de la estimación.
• La amplitud del IC depende:
  
• Nivel de confianza: grado de confianza de que el verdadero valor se sitúe en el intervalo obtenido (1-α).
• Variabilidad parámetro: proporción esperada (variable cualitativa) o varianza (variable cuantitativa).
• Número sujetos (n).

Cuanto menor sea la variabilidad del parámetro y mayor el número de sujetos, mayor precisión existirá en la estimación para un grado de confianza determinado.
Cuanta más confianza se desee obtener, más amplio será el IC y menor la precisión obtenida.
Los factores necesarios para el cálculo del tamaño muestral para la estimación de un parámetro serían:

• Variabilidad: otros estudios, datos propios, estudio piloto:
  
• Cualitativas: P x (1-P) (si tenemos dudas consideraremos que P=50%), donde P es el valor de la proporción que se supone existe en la población.
• Cuantitativas: varianza (s2).
• Precisión: amplitud del IC (fijada por el investigador).
  
• Nivel de confianza (1-α): grado de confianza de que el verdadero valor se sitúa en el intervalo obtenido (fijado por el investigador).
  

A continuación os presentamos algunas fórmulas empleadas para el cálculo del tamaño muestral adecuado para estimar un parámetro:

• Estimación de una proporción (variable cualitativa):
  
• N=Zα² P (1-P) / i²
• Estimación de una media (variable cuantitativa):
  
• N=Zα² s² / i²
  
  

N: número de sujetos necesarios. Zα: valor de Z correspondiente al riesgo fijado. P: valor de la proporción que se supone existe en la población. s2: varianza de la distribución de la variable cuantitativa que se supone que existe en la población. i: precisión con que se desea estimar el parámetro (2.i es la amplitud del I.C.).

• Corrección para poblaciones finitas:
  
• na=n / [1 + (n/N)]

Ejemplo: para calcular el porcentaje de diabéticos controlados en una zona básica de salud determinada.

na: número de sujetos necesarios. n: número de sujetos calculado para poblaciones infinitas. N: tamaño de la población finita.

Contraste de hipótesis: consideraciones

• Hipótesis nula (H0): no existen diferencias entre los grupos de comparación.
  
• Hipótesis alternativa (H1): sí hay diferencias entre los grupos de comparación.
  
• Tamaño muestral: hay que fijar a priori los riesgos que se está dispuesto a asumir de cometer los errores α y β.
  
• Incrementar el número considerando los abandonos/pérdidas de seguimiento que se producirán.

En la figura 18 se explican los errores en estudios que comparan dos grupos:


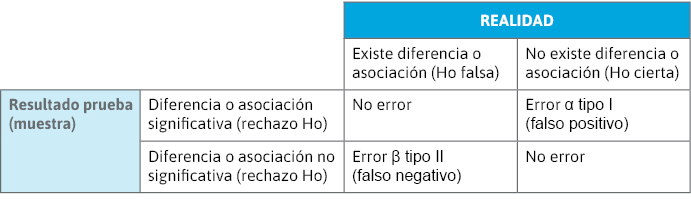
Figura 18. Tipos de error aleatorio de una prueba de contraste de hipótesis

Los factores necesarios para el cálculo del tamaño muestral para un contraste de hipótesis son:

• Hipótesis a contrastar:
  
• Bilaterales (dos colas): B ≠ A
• Unilaterales (una cola): B > A
• Riesgo o errores α y β:
  
• α (tipo I): 0,05 (5%).
• β (tipo II): 0,05-0,2 (5-20%).
• Poder o potencia estadística: probabilidad de detectar una diferencia cuando existe en la población (1 – β).
• Magnitud de la diferencia o asociación (d): mínima diferencia a detectar entre los grupos a comparar que sea clínicamente relevante:
  
• Cualitativas: P1-P2.
• Cuantitativas: x1-x2.
• Variabilidad de la variable de respuesta en los grupos:
  
• Cualitativas: P11-P1) y P2(1-P2).
• Cuantitativas: varianza en el grupo de referencia (s2).

P: valor de la proporción que se supone existe en la población.

A continuación os presentamos algunas fórmulas empleadas para el cálculo del tamaño muestral adecuado para realizar un contraste de hipótesis:

• Comparación de dos proporciones (v. cualitativa):
  
  
  
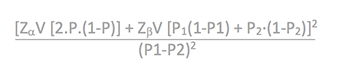
• Comparación de dos medias (v. cuantitativa):
  
• N=2(Z_α + Z_β)²s² / d²
  
  

N: número de sujetos necesarios en cada grupo. Zα y Zβ: valores de Z correspondientes a los riesgos α y β fijados. P1 y P2: valores de la proporción que se supone existe en los dos grupos. P2-P1: valor minimo de la diferencia que se desea detectar (variable cualitativa). P: media ponderada de las proporciones P1 y P2. s2: varianza de la distribución de la variable cuantitativa que se supone que existe en el grupo de referencia. d: valor mínimo de la diferencia que se desea detectar (variable cuantitativa).

• Contraste de hipótesis: equivalencia.
  
• Determinar si una nueva intervención (más económica, más tolerable, etc.) es tan eficaz como la terapéutica habitual.
• La diferencia entre las intervenciones debe ser menor que la mínima diferencia clínicamente relevante (d):
• N=2.P(1 – P)(Z_α + Z_β )² / d²
  
  

N: número de sujetos necesarios en cada grupo. Zα y Zβ: valores de Z correspondientes a los riesgos α y β fijados. P: proporción que se espera en el grupo control. d: diferencia máxima entre la eficacia de ambas intervenciones que se tolerará para concluir que son equivalentes.

• Corrección por las no respuestas, pérdidas y abandonos:
  
• Debe asegurarse que finalizará el estudio el número de pacientes requerido:
• Na=N [1 / (1 – R)]
  
  

N: número de sujetos teórico. Na: número de sujetos ajustado. R: proporción esperada de pérdidas.

Tamaño de la muestra: consideraciones generales

• Proporciona una cifra aproximada.
  
• Las asunciones deben ser justificadas.
  
• Estrategias para minimizar el número:
  
• Conseguir población más homogénea y disminuir la variabilidad: ajustar los criterios de inclusión, medidas repetidas, etc.
• Aumentar la frecuencia de aparición del fenómeno: población alto riesgo.
• Usar criterios de evaluación cuantitativos

Variables

Variable es toda característica medida en un estudio.

Las etapas a seguir son:

• Selección de las variables.
  
• Definición de las variables.
  
• Medición de las variables.
  

Selección de variables

Habrá que incorporar tantas como sea necesario y tan pocas como sea posible:

• Evaluar la aplicabilidad del protocolo: criterios selección.
  
• Factor de estudio y criterio de evaluación.
  
• Factores confusión y variables modificadoras del efecto.
  
• Universales o descriptoras de los sujetos.
  
• Otras: preguntas secundarias, tiempo, etc.
  

Tipo de variables

• Según interrelación:
  
• Dependiente o resultado: efecto que se quiere estudiar.
• Independientes o explicativas: causa o factor predictor del efecto (interactúan sobre el fenómeno a estudio). Preceden a la variable resultado:
• Universales.
• De confusión.
• Modificadoras de efecto.
• Según naturaleza:
  
• Cualitativas.
• Cuantitativas.

Podemos ver las variables de confusión/modificadoras (figura 19).


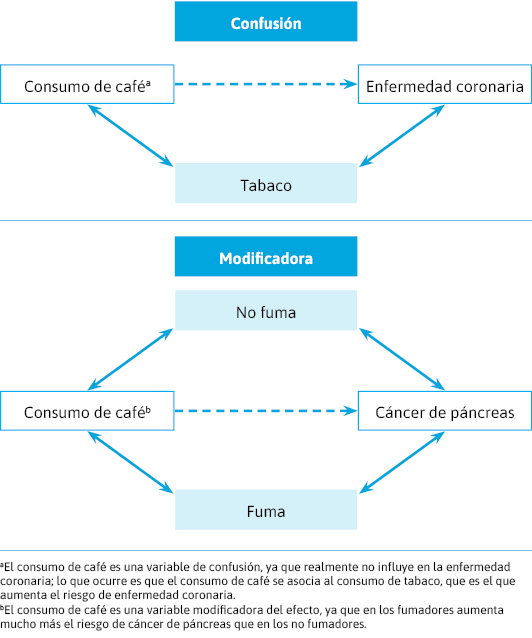
Figura 19. Variables de confusión/modificadoras

Variables universales

Características sociodemográficas:

• Sexo o edad: están ligadas íntimamente a la mayoría de los procesos que se van a estudiar, por lo que hay que considerarlas como FR o como potenciales factores de confusión.
  
• Otras: religión, paridad, grupo étnico o raza, etc. No suelen recogerse de manera rutinaria y su inclusión vendrá determinada por los objetivos específicos del estudio.
  

Definición de las variables

Las variables necesitan ser definidas operativamente para poder ser medidas.

La definición precisa y operativa de las variables permite que se mida lo que realmente se quiere medir (validez) y permite la reproductibilidad del estudio.

Se recomienda partir inicialmente de definiciones «conceptuales»:

• «Hipertensión» ⇒ «aumento de tensión arterial»
  
• «Obesidad» ⇒ «aumento de peso»
  

Pero tendríamos que preguntarnos:

• ¿Qué aumento de tensión consideramos hipertensión?
  
• ¿Cuántos kilos de más consideramos obesidad?
  

La definición operativa explica claramente lo que de verdad se va a medir, sin ambigüedades y con una sola posible interpretación:

• Hipertensión ⇒ presión diastólica > 90 mmHg y presión sistólica > 140 mmHg.
  
• Obesidad ⇒ índice de masa corporal (IMC) ≥ 30 kg/m².
  

Además, hay que tener en cuenta que la definición de cada variable debe ser:

• Clara y precisa.
  
• Utilizar definiciones estandarizadas siempre que sea posible.
  
• Prever todas las opciones (las distintas categorías deben ser excluyentes): por ejemplo: NS/NC.
  

Escalas de medida (tabla 4)

• Cualitativa/categórica:
  
• Nominal: sexo (H/M), hipertensión arterial (HTA) (S/N), estado civil (S, C, Sp, D, V, NC).
• Ordinal: clase social (alta/media/baja), disnea (no, leve, moderada, grave).
• Cuantitativa:
  
• Discreta (finita, enteros): frecuencia cardíaca, número de hijos.
• Continua (infinita, admite decimales): tensión arterial (TA), estatura.
• Constructos intangibles: calidad de vida, inteligencia, etc. ⇒ cuestionarios, etc.
  

Tabla 4. Ejemplo: definición de las variables

Estrategia de análisis de los datos

• Estudios descriptivos:
  
• Revisar los datos previamente al análisis.
• Describir los sujetos estudiados.
• Evaluar la representatividad de la muestra.
• Estimar el valor del parámetro de interés.
• Calcular el IC de la estimación.
• Describir las no respuestas y/o pérdidas de seguimiento y evaluar su impacto potencial.
• Análisis de subgrupos.
• Estudios analíticos:
  
• Revisar los datos previamente al análisis.
• Describir los sujetos estudiados.
• Evaluar la comparabilidad inicial de los grupos (ECC).
• Estimar la magnitud del efecto o asociación (OR, RR, etc.).
• Evaluar la existencia de modificación del efecto.
• Ajustar por potenciales factores de confusión.
• Análisis de subgrupos.
• Responder las preguntas secundarias.

Codificación/introducción de los datos:

• Programa de gestión de base de datos:
  
• ACCESS.
• EPIINFO.
• SPSS, etc.
• Mismo orden que recogida.
  
• Evitar errores:
  
• Filtros.
• Codificación segunda ocasión u otra persona.

Revisión de los datos:

• Estudiar las variables una a una:
  
• Valores no habituales o ilógicos.
• Errores en la transcripción.
• Consultar cuaderno de recogida de datos (CRD).

En el apartado de análisis de los datos es esencial describir cómo se va a realizar:

• Estadística descriptiva: distribución de frecuencias, medias, medianas, medidas de dispersión.
  
• Análisis simple (comparaciones entre las variables dos a dos):
  
• Patrón de relación entre las variables.
• Determinación de la significación de la asociación.
• Determinación de la magnitud de la asociación.
• Comparación de dos variables tomando en consideración otras variables (análisis estratificado, multivariante).
  

Siempre se debe comenzar describiendo la población de útil, lo que nos servirá para:

• Conocer en qué tipo de sujetos se ha observado el fenómeno estudiado.
  
• Comprobar que ambos grupos son comparables.
  
• Evaluar la validez externa.
  
• Permitir la replicabilidad del estudio.
  

Análisis descriptivo (tabla 5):

• Características:
  
• Sociodemográficas.
• Enfermedad y/o exposición.
• Situación basal.
  
• Factores estudiados.
  
• Estadística descriptiva:
  
• Cuantitativas: medidas de tendencia central (media), de dispersión (desviación típica o estándar), de posición (límites o rango), IC 95%, histograma.
• Cualitativas: frecuencias absolutas y relativas (%), IC 95%, diagrama de barras.

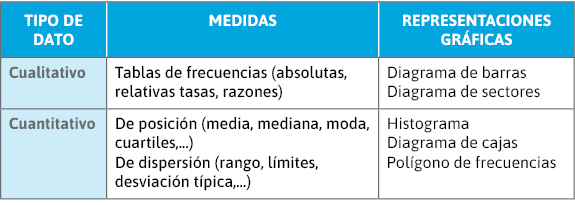
Tabla 5. Análisis descriptivo

A continuación, se realizarán análisis de inferencia estadística para determinar cuál es el valor de un parámetro poblacional a partir de lo observado en una muestra (extrapolamos nuestros datos a la población general).
El IC es aquel que tiene una elevada probabilidad de contener el verdadero valor poblacional. Cuanto más estrecho sea, más preciso será el resultado que obtengamos con nuestra muestra.

El análisis inferencial puede utilizarse para:

• Estimación de parámetros:
  
• Puntual.
• Por IC.
• Contraste de hipótesis:
  
• Errores aleatorios tipo I y II.
• Pruebas estadísticas:
• Análisis bivariante.
• Análisis multivariante.

Los factores de los que depende la elección de la prueba estadística adecuada son:

• Escala de medida de la variable de respuesta (dependiente).
  
• Escala de medida del factor de estudio (independiente).
  
• Carácter apareado o independiente de los datos.
  
• Condiciones de aplicación específicas de cada prueba:
  
• Número de observaciones.
• Asunciones sobre la distribución poblacional de las variables.

Pruebas estadísticas bivariantes

Se utilizan para analizar la asociación entre un factor de estudio (independiente) y una variable de respuesta (dependiente). Según el tipo de ambos factores, se deberá emplear una de las siguientes técnicas estadísticas:

• Ambos cualitativos: ji cuadrado o test exacto de Fisher.
  
• Comparación de dos grupos respecto a una variable cuantitativa: t de Student o U de Mann-Whitney.
  
• Comparación de más de dos grupos respecto a una variable cuantitativa: ANOVA o Kruskal-Wallis.
  
• Ambos cuantitativos: correlación de Pearson o de Spearman:
  
• Si se asume una relación de dependencia lineal de una de las variables respecto a la otra: regresión lineal simple.

En la tabla 6 se muestran los distintos test de contraste de hipótesis bivariantes disponibles para explorar diferencias significativas en determinadas variables entre grupos de pacientes o para identificar relación (asociación) entre dos variables en los sujetos de nuestro estudio. Identificando el tipo de datos que quieren compararse, es sencillo elegir el test más adecuado. La interpretación final de todos ellos es idéntica (un valor p < 0,05 identifica asociación o diferencias significativas).
No hay que olvidar que las comparaciones de datos apareados necesitan test de contraste propios, que tienen en cuenta la mayor homogeneidad de los sujetos comparados.


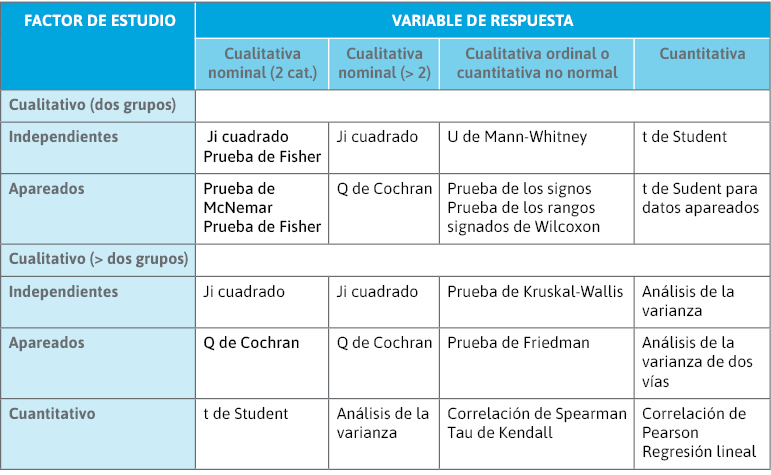
Tabla 6. Distintos test de contraste de hipótesis bivariantes

Pruebas estadísticas multivariantes

Se emplean para estudiar la relación entre una variable dependiente (respuesta) y múltiples variables independientes (factor de estudio y otras variables a controlar). Pueden tener una de las siguientes finalidades:

• Predicción: obtener una ecuación que permita, conociendo los valores de un conjunto de variables independientes, predecir el valor de la variable dependiente.
  
• Descripción de la relación entre variables: identificar qué variables están asociadas con la variable dependiente.
  
• Estimación: obtener una estimación del efecto del factor de estudio sobre la variable de respuesta, controlando la influencia de variables de confusión.
  

A continuación se resumen las características de las pruebas multivariantes más utilizadas (tabla 7):

• Regresión lineal múltiple:
  
• Tanto la variable dependiente como las independientes son cuantitativas (aunque algunas independientes pueden ser cualitativas).
• El valor de un coeficiente es una estimación del efecto de la variable independiente sobre la dependiente, ajustado por el resto de las variables independientes.
• Representa el cambio esperado de la variable dependiente cuando se incrementa en una unidad el valor de la variable independiente, asumiendo que el resto de las variables se mantienen constantes.
• Regresión logística:
  
• La variable dependiente es dicotómica
• El valor de cada coeficiente estima medidas relativas, tal como la OR asociada al factor de estudio y ajustada por el resto de variables independientes.
• Los coeficientes no pueden interpretarse directamente. Por ejemplo, para un coeficiente de 0,12, su OR sería de 0,12=1,13.
• Regresión de Cox:
  
• La variable dependiente es el tiempo de supervivencia o el tiempo transcurrido hasta la aparición de un desenlace determinado.

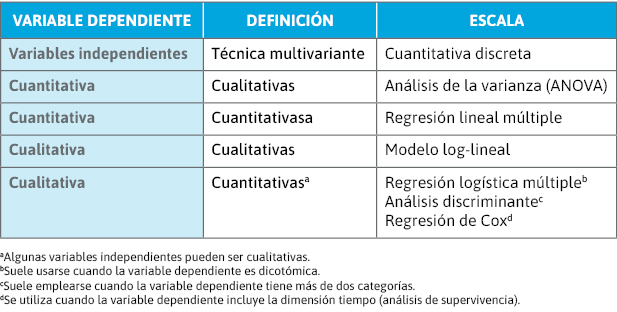
Tabla 7. Características de las pruebas multivariantes más utilizadas